 Reading Time: 5 minutes read
Reading Time: 5 minutes readما هو معامل ارتباط بيرسون؟
يُعرَّف معامل ارتباط بيرسون أو معامل ارتباط بيرسون أو معامل ارتباط بيرسون في الإحصاء على أنه قياس قوة العلاقة بين متغيرين وارتباطهما ببعضهما البعض.
بكلمات بسيطة ، يحسب معامل ارتباط بيرسون تأثير التغيير في متغير واحد عندما يتغير المتغير الآخر.
فمثلا: حتى سن معينة ، (في معظم الحالات) سيستمر ارتفاع الطفل مع زيادة عمره. بالطبع ، يعتمد نموه / نموها على عوامل مختلفة مثل الجينات والموقع والنظام الغذائي ونمط الحياة وما إلى ذلك.
يعتمد هذا النهج على التغاير وبالتالي فهو أفضل طريقة لقياس العلاقة بين متغيرين.
ماذا يفعل اختبار معامل ارتباط بيرسون؟
ارتباط معامل بيرسون له دلالة إحصائية عالية. يبحث في العلاقة بين متغيرين. يسعى إلى رسم خط من خلال بيانات متغيرين لإظهار علاقتهما. يتم قياس علاقة المتغيرات بمساعدة حاسبة معامل ارتباط بيرسون. يمكن أن تكون هذه العلاقة الخطية موجبة أو سلبية.
على سبيل المثال:
- العلاقة الخطية الإيجابية: في معظم الحالات ، بشكل عام ، يزيد دخل الشخص مع زيادة عمره / عمرها.
- علاقة خطية سالبة: إذا زادت المركبة من سرعتها ، يقل الوقت المستغرق في السفر ، والعكس صحيح.
من المثال أعلاه ، من الواضح أن معامل ارتباط بيرسون ، ص ، يحاول اكتشاف شيئين – قوة واتجاه العلاقة من أحجام العينة المحددة.
صيغة معامل ارتباط بيرسون
تكتشف صيغة معامل الارتباط العلاقة بين المتغيرات. تقوم بإرجاع القيم بين -1 و 1. استخدم حاسبة ارتباط معامل بيرسون أدناه لقياس قوة متغيرين.
صيغة معامل ارتباط بيرسون:
أين:
N = عدد أزواج الدرجات
Σxy = مجموع منتجات الدرجات المزدوجة
Σx = مجموع نقاط x
Σy = مجموع درجات y
Σ x 2 = مجموع نقاط x التربيعية
Σy 2 = مجموع نقاط y التربيعية
حاسبة معامل ارتباط بيرسون
إليك دليل خطوة بخطوة لحساب معامل ارتباط بيرسون:
الخطوةالاولى: قم بإنشاء جدول معامل ارتباط بيرسون. قم بعمل مخطط بيانات ، متضمنًا كلا المتغيرين. قم بتسمية هذه المتغيرات “x” و “y”. أضف ثلاثة أعمدة إضافية – (س ص) و (س ^ 2) و (ص ^ 2). الرجوع إلى مخطط البيانات البسيط هذا.
الخطوة الثانية: استخدم الضرب الأساسي لإكمال الجدول.
الخطوة الثالثة: أضف جميع الأعمدة من الأسفل إلى الأعلى.
الخطوة الرابعة: استخدم صيغة الارتباط لتعويض القيم.
إذا كانت النتيجة سلبية ، فهناك علاقة ارتباط سلبية بين المتغيرين. إذا كانت النتيجة موجبة ، فهناك علاقة ارتباط موجبة بين المتغيرات. يمكن أن تحدد النتائج أيضًا قوة العلاقة الخطية ، أي علاقة إيجابية قوية ، علاقة سلبية قوية ، علاقة إيجابية متوسطة ، وما إلى ذلك.
تحديد قوة معامل الارتباط اللحظي لحاصل الضرب Pearson
يحدد معامل الارتباط اللحظي للمنتج ، أو معامل ارتباط بيرسون أو ارتباط معامل بيرسون ص ، قوة العلاقة الخطية بين متغيرين. كلما كان الارتباط أقوى بين المتغيرين ، كلما كانت إجابتك أقرب إلى 1 أو -1. يشير الحصول على قيم 1 أو -1 إلى أن جميع نقاط البيانات مخططة على خط مستقيم من “أفضل ملاءمة”. وهذا يعني أن التغيير في عوامل أي متغير لا يضعف الارتباط مع المتغير الآخر. كلما اقتربت إجابتك من 0 ، زاد التباين في المتغيرات.
كيف نفسر معامل ارتباط بيرسون
فيما يلي الإرشادات المقترحة لتفسير ارتباط معامل بيرسون:
لاحظ أن قوة ارتباط المتغيرات تعتمد على ما تقيسه وأحجام العينة.
على الرسم البياني ، يمكن للمرء أن يلاحظ العلاقة بين المتغيرات ووضع افتراضات قبل حسابها. تظهر المخططات المبعثرة ، إذا كانت قريبة من الخط ، علاقة قوية بين المتغيرات. وكلما اقتربت المخططات المبعثرة بجانب الخط ، زادت قوة علاقة المتغيرات. كلما ابتعدوا عن الخط ، أصبحت العلاقة أضعف. إذا كان الخط موازيًا لمحور x تقريبًا ، نظرًا لوجود مخططات التشتت بشكل عشوائي على الرسم البياني ، فمن الآمن افتراض عدم وجود ارتباط بين المتغيرين.
ماذا يعني مصطلح القوة والاتجاه؟
مصطلح “القوة” و “الاتجاه” لهما دلالة إحصائية. فيما يلي شرح مباشر لكلمتين:
- قوة: تشير القوة إلى علاقة العلاقة بين متغيرين. هذا يعني مدى ثبات متغير واحد سيتغير بسبب التغيير في الآخر. تشير القيم القريبة من +1 أو -1 إلى علاقة قوية. يتم تحقيق هذه القيم إذا كانت نقاط البيانات تقع على الخط أو قريبة جدًا منه. كلما ابتعدت نقاط البيانات ، كانت قوة العلاقة الخطية أضعف. عندما لا توجد طريقة عملية لرسم خط مستقيم لأن نقاط البيانات مبعثرة ، تكون قوة العلاقة الخطية هي الأضعف.
- اتجاه: يشير اتجاه الخط إلى علاقة خطية موجبة أو سالبة بين المتغيرات. إذا كان للخط منحدر صاعد ، فإن المتغيرات لها علاقة موجبة. هذا يعني أن الزيادة في قيمة أحد المتغيرات ستؤدي إلى زيادة قيمة المتغير الآخر. الارتباط السلبي يصور منحدرًا هبوطيًا. هذا يعني أن الزيادة في مقدار متغير واحد تؤدي إلى انخفاض قيمة متغير آخر.
أمثلة على معامل ارتباط بيرسون
لنلقِ نظرة على بعض الأمثلة المرئية لمساعدتك في تفسير جدول معامل ارتباط بيرسون:
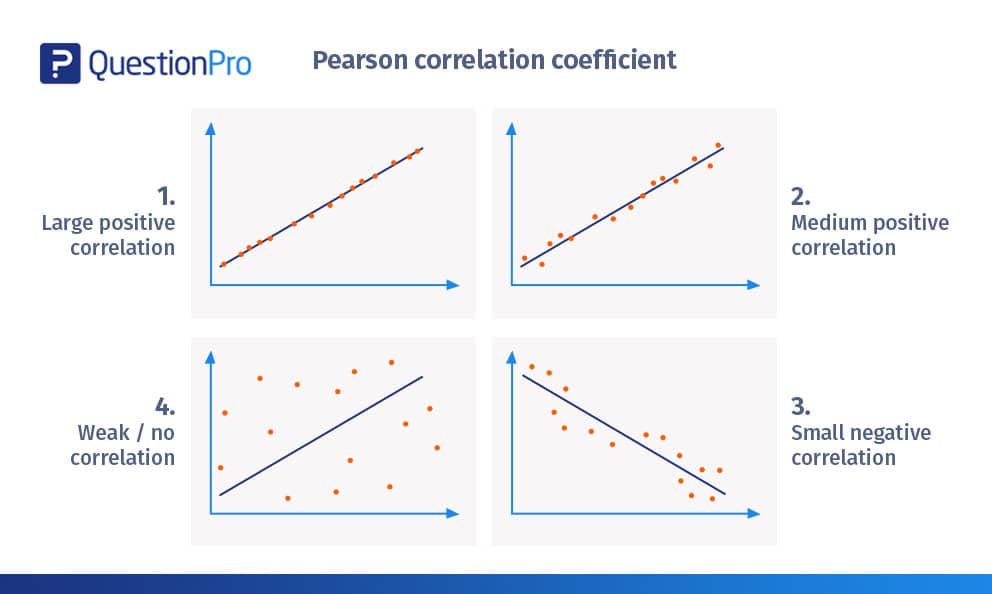
- ارتباط إيجابي كبير:
يوضح الشكل أعلاه ارتباطًا تقريبًا +1.
يتم رسم مخططات التشتت تقريبًا على الخط المستقيم.
المنحدر موجب ، مما يعني أنه إذا زاد أحد المتغيرات ، فإن المتغير الآخر يزيد أيضًا ، مما يظهر خطًا خطيًا موجبًا.
هذا يدل على أن التغيير في متغير واحد يتناسب طرديا مع التغيير في المتغير الآخر.
من الأمثلة على الارتباط الإيجابي الكبير – مع نمو الأطفال ، تزداد أحجام ملابسهم وأحذيتهم.
لنلقِ نظرة على بعض الأمثلة المرئية لمساعدتك في تفسير جدول معامل ارتباط بيرسون:
- ارتباط إيجابي متوسط:
يوضح الشكل أعلاه ارتباطًا إيجابيًا.
الارتباط أعلى من +0.8 ولكن أقل من 1+.
يظهر نمط صعود خطي قوي جدًا.
مثال على الارتباط الإيجابي المتوسط – مع زيادة عدد السيارات ، يزداد الطلب في متغير الوقود.
- ارتباط سلبي صغير
في الشكل أعلاه ، مخططات التبعثر ليست قريبة من الخط المستقيم مقارنة بالأمثلة السابقة
يُظهر ارتباطًا خطيًا سالبًا يبلغ -0.5 تقريبًا
التغيير في متغير واحد يتناسب عكسيا مع تغير المتغير الآخر حيث يكون الميل سالب.
مثال على ارتباط سلبي صغير سيكون – كلما أكل شخص ما ، كلما قل الجوع.
- ضعف / عدم وجود ارتباط
المخططات المبعثرة بعيدة عن الخط.
من الصعب عملياً رسم خط.
الارتباط يقارب +0.15
لا يمكن الحكم على أن التغيير في متغير واحد يتناسب طرديا أو يتناسب عكسيا مع المتغير الآخر.
مثال على ضعف / عدم وجود ارتباط سيكون – تؤدي الزيادة في أسعار الوقود إلى تقليل عدد الأشخاص الذين يتبنون حيوانات أليفة.



















