 Reading Time: 7 minutes read
Reading Time: 7 minutes read
Il est habituel de quantifier les relations linéaires à l’aide du coefficient de corrélation de Pearson. Pour indiquer la force et la direction de la connexion entre deux variables, il prend une valeur comprise entre -1 et 1.
Il peut aider les investisseurs à se diversifier. Les calculs effectués à partir de diagrammes de dispersion des rendements historiques entre des paires d’actifs, telles que les actions et les obligations, les actions et les matières premières, les obligations et l’immobilier, etc.
Nous allons donc nous familiariser avec le coefficient de corrélation de Pearson et savoir comment mesurer la relation entre deux variables liées à l’aide de ce coefficient.
Qu’est-ce que le coefficient de corrélation de Pearson ?
Le coefficient de corrélation de Pearson ou coefficient de corrélation de Pearson ou r de Pearson est défini en statistique comme la mesure de la force de la relation entre deux variables et leur association l’une avec l’autre.
En d’autres termes, le coefficient de corrélation de Pearson calcule l’effet du changement d’une variable lorsque l’autre variable change.
Par exemple : Jusqu’à un certain âge (dans la plupart des cas), la taille d’un enfant augmente au fur et à mesure que son âge augmente. Bien entendu, sa croissance dépend de divers facteurs tels que les gènes, le lieu, le régime alimentaire, le mode de vie, etc.
Cette approche est basée sur la covariance et constitue donc la meilleure méthode pour mesurer la relation entre deux variables.
À quoi sert le test du coefficient de corrélation de Pearson ?
La corrélation du coefficient de Pearson a une signification statistique élevée. Elle étudie la relation entre deux variables. Elle vise à tracer une ligne à travers les données de deux variables pour montrer leur relation. La relation entre les variables est mesurée à l’aide de la calculatrice du coefficient de corrélation de Pearson. Cette relation linéaire peut être positive ou négative.

Par exemple :
- Relation linéaire positive : Dans la plupart des cas, universellement, le revenu d’une personne augmente avec son âge.
- Relation linéaire négative : Si le véhicule augmente sa vitesse, le temps de parcours diminue, et inversement.
L’exemple ci-dessus montre que le coefficient de corrélation de Pearson, r, tente de déterminer deux choses : la force et la direction de la relation à partir d’échantillons de taille donnée.
Formule et calcul du coefficient de corrélation de Pearson
La formule du coefficient de corrélation permet de déterminer la relation entre les variables. Il renvoie les valeurs comprises entre -1 et 1. Utilisez la calculatrice de corrélation du coefficient de Pearson ci-dessous pour mesurer la force de deux variables.
Formule du coefficient de corrélation de Pearson :

Où ?
N = le nombre de paires de notes
Σxy = la somme des produits des notes appariées
Σx = la somme des notes x
Σy = la somme des notes y
Σx2 = la somme des scores x au carré
Σy2 = la somme des scores y au carré
Calcul
Voici un guide étape par étape pour calculer le coefficient de corrélation de Pearson :
Première étape : Créez un tableau des coefficients de corrélation.
Créez un graphique de données, incluant les deux variables. Nommez ces variables « x » et « y ». Ajoutez trois colonnes supplémentaires : (xy), (x^2) et (y^2). Reportez-vous à ce simple tableau de données.

Deuxième étape : Utilisez la multiplication de base pour compléter le tableau.

Troisième étape : Additionnez toutes les colonnes de bas en haut.

Quatrième étape : Utilisez la formule de corrélation pour introduire les valeurs.
Si le résultat est négatif, il existe une relation de corrélation négative entre les deux variables. Si le résultat est positif, il existe une relation de corrélation positive entre les variables. Les résultats peuvent également définir la force d’une relation linéaire, c’est-à-dire une relation positive forte, une relation négative forte, une relation positive moyenne, etc.
Détermination de la force du coefficient de corrélation produit-moment de Pearson
Le coefficient de corrélation produit-moment de Pearson, ou simplement le coefficient de corrélation de Pearson ou le coefficient de corrélation r de Pearson, détermine la force de la relation linéaire entre deux variables.
Plus l’association entre les deux variables est forte, plus votre réponse penchera vers 1 ou -1. L’obtention de valeurs de 1 ou -1 signifie que tous les points de données sont tracés sur la ligne droite du « meilleur ajustement ». Cela signifie que la modification des facteurs d’une variable n’affaiblit pas la corrélation avec l’autre variable. Plus votre réponse est proche de 0, plus les variables varient.
Comment interpréter le coefficient de corrélation de Pearson
Les lignes directrices proposées pour l’interprétation de la corrélation du coefficient de Pearson sont présentées ci-dessous :
Notez que la force de l’association des variables dépend de ce que vous mesurez et de la taille des échantillons.
Sur un graphique, on peut remarquer la relation entre les variables et faire des hypothèses avant même de les calculer. Les diagrammes de dispersion, s’ils sont proches de la ligne, montrent une forte relation entre les variables.
Plus les diagrammes de dispersion sont proches de la ligne, plus la relation entre les variables est forte. Plus ils s’éloignent de la ligne, plus la relation s’affaiblit. Si la ligne est presque parallèle à l’axe des x en raison des nuages de points placés au hasard sur le graphique, on peut supposer qu’il n’y a pas de corrélation entre les deux variables.
Que signifient les termes « force » et « direction » ?
Les termes « force » et « direction » ont une signification statistique. Voici une explication simple de ces deux mots :
- La force : La force signifie la corrélation de la relation entre deux variables. Il s’agit du degré de variation d’une variable en fonction de la variation de l’autre. Les valeurs proches de +1 ou -1 indiquent une relation forte. Ces valeurs sont atteintes si les points de données tombent sur la ligne ou en sont très proches.
Plus les points de données s’éloignent, plus la force de la relation linéaire est faible. Lorsqu’il n’est pas possible de tracer une ligne droite parce que les points de données sont dispersés, la force de la relation linéaire est la plus faible. - Direction : La direction de la ligne indique une relation linéaire positive ou négative entre les variables. Si la ligne a une pente ascendante, les variables ont une relation positive.
Cela signifie qu’une augmentation de la valeur d’une variable entraînera une augmentation de la valeur de l’autre variable. Une corrélation négative indique une pente descendante. Cela signifie qu’une augmentation de la quantité d’une variable entraîne une diminution de la valeur d’une autre variable.
Exemples de coefficient de corrélation de Pearson
Voyons quelques exemples visuels pour vous aider à interpréter le tableau des coefficients de corrélation :
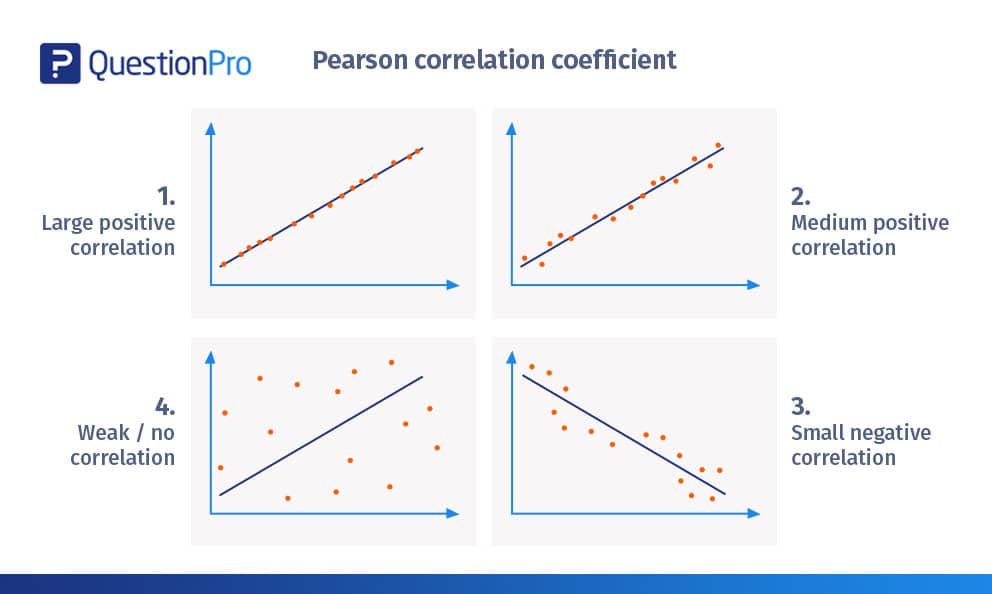
Corrélation positive importante
- La figure ci-dessus montre une corrélation de près de +1.
- Les diagrammes de dispersion sont presque en ligne droite.
- La pente est positive, ce qui signifie que si une variable augmente, l’autre variable augmente également, ce qui indique une ligne linéaire positive.
- Cela signifie que la variation d’une variable est directement proportionnelle à la variation de l’autre variable.
- Voici un exemple de corrélation positive importante : – Les enfants grandissent, tout comme leurs vêtements et leurs chaussures.
Corrélation positive moyenne
- La figure ci-dessus montre une corrélation positive.
- La corrélation est supérieure à +0,8 mais inférieure à 1+.
- Elle montre une tendance linéaire assez forte à la hausse.
- Voici un exemple de corrélation positive moyenne : – L’augmentation du nombre d’automobiles entraîne une augmentation de la demande de la variable « carburant ».
Faible corrélation négative
- Dans la figure ci-dessus, les diagrammes de dispersion ne sont pas aussi proches de la ligne droite que dans les exemples précédents.
- Elle présente une corrélation linéaire négative d’environ -0,5
- La variation d’une variable est inversement proportionnelle à la variation de l’autre variable, la pente étant négative.
- Un exemple de petite corrélation négative serait – Plus quelqu’un mange, moins il a faim.
Corrélation faible / inexistante
- Les diagrammes de dispersion sont très éloignés de la ligne.
- Il est difficile de tracer une ligne dans la pratique.
- La corrélation est d’environ +0,15
- On ne peut pas juger que le changement d’une variable est directement proportionnel ou inversement proportionnel à l’autre variable.
- Un exemple de corrélation faible/absente serait le suivant : une augmentation du prix des carburants entraîne une diminution du nombre de personnes qui adoptent des animaux de compagnie.
Conclusion
Le coefficient de corrélation de Pearson peut être déterminé en collectant des données sur deux variables d’intérêt au moyen d’une enquête. Vous pouvez l’utiliser pour savoir si la corrélation entre les deux variables est positive ou négative et si elle est forte.
QuestionPro Research Suite est une suite d’outils permettant de tirer parti de la recherche et de transformer les informations qui peuvent être utilisées pour collecter des données pour l’analyse du coefficient de corrélation de Pearson. Après avoir exporté les données d’enquête de QuestionPro et les avoir importées dans un tableur ou une application statistique, vous pouvez effectuer l’analyse de corrélation.
QuestionPro offre des outils d’analyse de données utiles tels que les tableaux croisés, la visualisation des données et les tests statistiques, en plus du calcul du coefficient de corrélation. Ces qualités peuvent vous aider dans votre recherche et dans la compréhension des relations entre vos variables.
Prêt à découvrir la relation entre vos variables et à faire progresser l’analyse de vos données ? Commencez dès aujourd’hui un essai gratuit de QuestionPro pour voir comment notre logiciel d’enquête peut vous aider à déterminer facilement le coefficient de corrélation de Pearson. Ne manquez pas cette occasion d’améliorer l’analyse des données et la recherche.














