 Reading Time: 13 minutes read
Reading Time: 13 minutes read
L’analyse de régression est peut-être l’une des méthodes statistiques les plus utilisées pour étudier ou estimer la relation entre un ensemble de variables indépendantes et dépendantes. Dans l’analyse statistique, il est essentiel de faire la distinction entre les données catégorielles et les données numériques, car les données catégorielles impliquent des catégories ou des étiquettes distinctes, tandis que les données numériques consistent en des quantités mesurables.
Il est également utilisé comme terme générique pour les différentes techniques d’analyse des données utilisées dans une méthode de recherche qualitative pour modéliser et analyser de nombreuses variables. Dans la méthode de régression, la variable dépendante est un prédicteur ou un élément explicatif, et la variable dépendante est le résultat ou une réponse à une requête spécifique.
APPRENDRE SUR : Les méthodes d’analyse statistique
Définition de l’analyse de régression
L’analyse de régression est souvent utilisée pour modéliser ou analyser des données. La plupart des analystes d’enquêtes l’utilisent pour comprendre la relation entre les variables, qui peut ensuite être utilisée pour prédire le résultat précis.
Exemple – Supposons qu’une entreprise de boissons non alcoolisées souhaite étendre son unité de production à un nouveau site. Avant d’aller de l’avant, l’entreprise souhaite analyser son modèle de génération de revenus et les différents facteurs susceptibles de l’influencer. L’entreprise mène donc une enquête en ligne à l’aide d’un questionnaire spécifique.
Après avoir utilisé l’analyse de régression, il devient plus facile pour l’entreprise d’analyser les résultats de l’enquête et de comprendre la relation entre différentes variables telles que l’électricité et le chiffre d’affaires – ici, le chiffre d’affaires est la variable dépendante.
APPRENEZ-EN DAVANTAGE SUR LE SUJET : Niveau d’analyse
En outre, la compréhension de la relation entre différentes variables indépendantes, telles que la tarification, le nombre de travailleurs et la logistique, et le chiffre d’affaires permet à l’entreprise d’estimer l’impact de divers facteurs sur les ventes et les bénéfices.
Les enquêteurs utilisent souvent cette technique pour examiner et trouver une corrélation entre différentes variables d’intérêt. Elle permet d’évaluer l’influence de différentes variables indépendantes sur une variable dépendante.
Dans l’ensemble, l’analyse de régression permet aux enquêteurs d’économiser des efforts supplémentaires en organisant plusieurs variables indépendantes dans des tableaux et en testant ou en calculant leur effet sur une variable dépendante. Différents types de méthodes de recherche analytique sont largement utilisés pour évaluer les nouvelles idées commerciales et prendre des décisions en connaissance de cause.
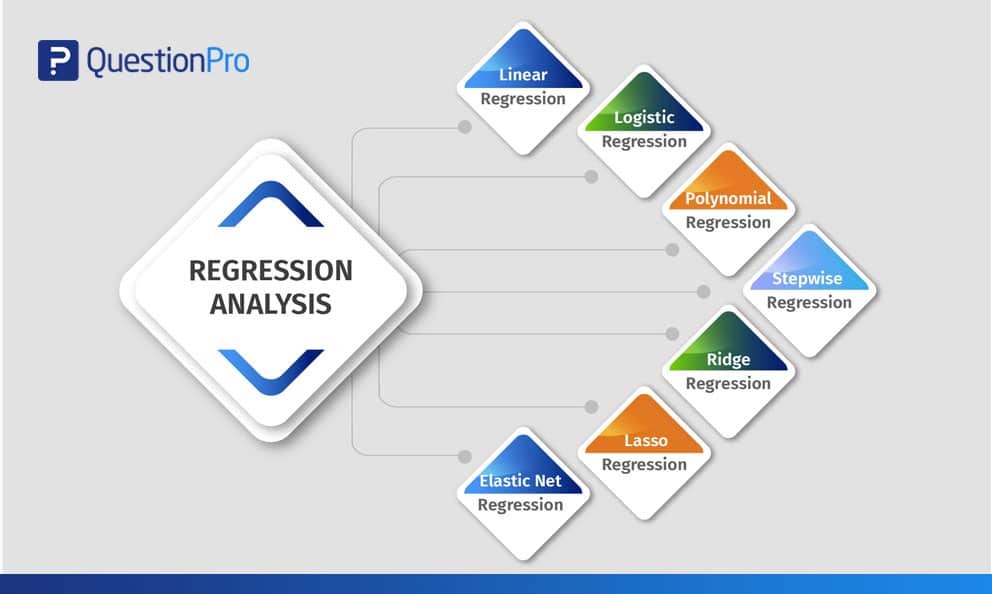
Types d’analyse de régression
Les chercheurs commencent généralement par apprendre la régression linéaire et logistique. En raison de la connaissance généralisée de ces deux méthodes et de leur facilité d’application, de nombreux analystes pensent qu’il n’existe que deux types de modèles. Chaque modèle a sa propre spécialité et sa propre capacité à fonctionner si des conditions spécifiques sont remplies.
Ce blog explique les sept types de méthodes d’analyse de régression multiple couramment utilisées pour interpréter les données de recensement dans différents formats.
01. Analyse de régression linéaire
C’est l’une des techniques de modélisation les plus connues, car elle fait partie des premières méthodes d’analyse de régression d’élite utilisées par les gens au moment de l’apprentissage de la modélisation prédictive. Ici, la variable dépendante est continue et la variable indépendante est plus souvent continue ou discrète avec une ligne de régression linéaire.
Veuillez noter que la régression linéaire multiple comporte plus d’une variable indépendante que la régression linéaire simple. Par conséquent, la régression linéaire ne doit être utilisée que lorsqu’il existe une relation linéaire entre la variable indépendante et la variable dépendante.
Exemple
Une entreprise peut utiliser la régression linéaire pour mesurer l’efficacité des campagnes de marketing, des prix et des promotions sur les ventes d’un produit. Supposons qu’une entreprise vendant des équipements sportifs veuille savoir si les fonds qu’elle a investis dans le marketing et l’image de marque de ses produits lui ont rapporté des bénéfices substantiels ou non.
La régression linéaire est la meilleure méthode statistique pour interpréter les résultats. L’avantage de la régression linéaire est qu’elle permet également d’analyser l’impact obscur de chaque activité de marketing et de stratégie de marque, tout en contrôlant le potentiel des composants à réguler les ventes.
Si l’entreprise mène simultanément deux ou plusieurs campagnes publicitaires, l’une à la télévision et les deux autres à la radio, la régression linéaire permet d’analyser facilement l’influence indépendante et combinée de la diffusion simultanée de ces publicités.
APPRENEZ-EN DAVANTAGE SUR LES PROJETS D’ANALYSE DE DONNÉES : Projets d’analyse de données
02. Analyse de régression logistique
La régression logistique est couramment utilisée pour déterminer la probabilité de réussite ou d’échec d’un événement. La régression logistique est utilisée lorsque la variable dépendante est binaire, comme 0/1, Vrai/Faux ou Oui/Non. On peut donc dire que la régression logistique est utilisée pour analyser soit les questions fermées d’une enquête, soit les questions exigeant des réponses numériques dans une enquête.
Veuillez noter que la régression logistique ne nécessite pas de relation linéaire entre une variable dépendante et une variable indépendante, tout comme la régression linéaire. La régression logistique applique une transformation logarithmique non linéaire pour prédire le rapport de cotes ; elle traite donc facilement divers types de relations entre une variable dépendante et une variable indépendante.
Exemple
La régression logistique est largement utilisée pour analyser les données catégorielles, en particulier pour les données à réponse binaire dans la modélisation des données commerciales. Plus souvent, la régression logistique est utilisée lorsque la variable dépendante est catégorique, par exemple pour prédire si l’allégation de santé faite par une personne est réelle(1) ou frauduleuse, pour comprendre si la tumeur est maligne(1) ou non.
Les entreprises utilisent la régression logistique pour prédire si les consommateurs d’un groupe démographique particulier achèteront leur produit ou s’ils achèteront à leurs concurrents en fonction de l’âge, du revenu, du sexe, de la race, de l’état de résidence, d’un achat antérieur, etc.
03. Analyse de régression polynomiale
La régression polynomiale est couramment utilisée pour analyser des données curvilignes lorsque la puissance d’une variable indépendante est supérieure à 1. Dans cette méthode d’analyse de régression, la ligne la mieux adaptée n’est jamais une « ligne droite », mais toujours une « ligne courbe » qui s’adapte aux points de données.
Veuillez noter qu’il est préférable d’utiliser la régression polynomiale lorsque deux variables ou plus ont des exposants et que quelques-unes n’en ont pas.
En outre, il peut modéliser des données séparables non linéaires en offrant la liberté de choisir l’exposant exact pour chaque variable, et ce avec un contrôle total sur les fonctions de modélisation disponibles.
Exemple
Combinée à l’analyse de la surface de réponse, la régression polynomiale est considérée comme l’une des méthodes statistiques sophistiquées couramment utilisées dans la recherche sur le retour d’information multisource. La régression polynomiale est surtout utilisée dans les secteurs de la finance et de l’assurance où la relation entre les variables dépendantes et indépendantes est curviligne.
Supposons qu’une personne veuille budgétiser ses dépenses en déterminant le temps nécessaire pour gagner une somme définitive. La régression polynomiale, en prenant en compte ses revenus et en prévoyant ses dépenses, peut facilement déterminer le temps précis qu’il doit travailler pour gagner cette somme spécifique.
04. Analyse de régression par étapes
Il s’agit d’un processus semi-automatisé qui permet de construire un modèle statistique en ajoutant ou en supprimant la variable dépendante sur la base des statistiques t de leurs coefficients estimés.
Si elle est utilisée correctement, la régression pas à pas vous permettra de disposer de données plus puissantes que n’importe quelle autre méthode. Elle fonctionne bien lorsque vous travaillez avec un grand nombre de variables indépendantes. Il ne fait qu’affiner le modèle d’unité d’analyse en piquant des variables au hasard.
Il est recommandé d’utiliser l’analyse de régression par étapes lorsqu’il y a plusieurs variables indépendantes, la sélection des variables indépendantes se faisant automatiquement sans intervention humaine.
Veuillez noter que dans la modélisation de régression par étapes, la variable est ajoutée ou soustraite de l’ensemble des variables explicatives. L’ensemble des variables ajoutées ou supprimées est choisi en fonction des statistiques de test du coefficient estimé.
Exemple
Supposons que vous disposiez d’un ensemble de variables indépendantes telles que l’âge, le poids, la surface corporelle, la durée de l’hypertension, le pouls de base et l’indice de stress, dont vous souhaitez analyser l’impact sur la tension artérielle.
Dans la régression par étapes, le meilleur sous-ensemble de la variable indépendante est automatiquement choisi ; il commence soit par ne choisir aucune variable pour continuer (en ajoutant une variable à la fois), soit par toutes les variables du modèle et procède à rebours (en supprimant une variable à la fois).
Ainsi, l’analyse de régression permet de calculer l’impact de chaque variable ou d’un groupe de variables sur la pression artérielle.
05. Analyse de régression de la crête
La régression ridge est basée sur la méthode des moindres carrés ordinaires qui est utilisée pour analyser des données multicollinéaires (données où les variables indépendantes sont fortement corrélées). La colinéarité peut être expliquée comme une relation quasi linéaire entre les variables.
En cas de multicolinéarité, les estimations des moindres carrés ne seront pas biaisées, mais si la différence entre elles est plus importante, elle peut être très éloignée de la valeur réelle. Cependant, la régression ridge élimine les erreurs standard en ajoutant un certain degré de biais aux estimations de régression dans le but de fournir des estimations plus fiables.
Si vous le souhaitez, vous pouvez également vous informer sur les biais de sélection en consultant notre blog.
Veuillez noter que les hypothèses dérivées de la régression ridge sont similaires à celles de la régression des moindres carrés, la seule différence étant la normalité. Bien que la valeur du coefficient soit restreinte dans la régression ridge, elle n’atteint jamais zéro, ce qui suggère l’incapacité de sélectionner les variables.
Exemple
Supposons que vous soyez fasciné par deux guitaristes qui se produisent en direct lors d’un événement près de chez vous, et que vous alliez assister à leur performance dans le but de savoir qui est le meilleur guitariste. Mais lorsque le spectacle commence, on remarque que les deux musiciens jouent des notes noires et bleues en même temps.
Est-il possible de déterminer le meilleur guitariste ayant le plus grand impact sur le son parmi eux lorsqu’ils jouent tous les deux fort et vite ? Comme ils jouent tous deux des notes différentes, il est très difficile de les différencier, ce qui en fait le meilleur cas de multicolinéarité, qui tend à augmenter les erreurs standard des coefficients.
La régression ridge permet de remédier à la multicolinéarité dans de tels cas et inclut un biais ou une estimation de réduction pour dériver les résultats.
06. Analyse de régression Lasso
Lasso (Least Absolute Shrinkage and Selection Operator) est similaire à la régression ridge, mais il utilise un biais en valeur absolue au lieu du biais carré utilisé dans la régression ridge.
Il a été développé en 1989 comme alternative à l’estimation traditionnelle des moindres carrés dans le but de déduire la majorité des problèmes liés à l’ajustement excessif lorsque les données comportent un grand nombre de variables indépendantes.
Lasso a la capacité de faire les deux – sélectionner les variables et les régulariser avec un seuil doux. L’application de la régression lasso facilite la dérivation d’un sous-ensemble de prédicteurs à partir de la minimisation des erreurs de prédiction lors de l’analyse d’une réponse quantitative.
Veuillez noter que les coefficients de régression atteignant la valeur zéro après le rétrécissement sont exclus du modèle lasso. Au contraire, les coefficients de régression dont la valeur est supérieure à zéro sont fortement associés aux variables de réponse, les variables explicatives pouvant être soit quantitatives, soit catégorielles, soit les deux.
Exemple
Supposons qu’une entreprise automobile souhaite effectuer une recherche sur la consommation moyenne de carburant des voitures aux États-Unis. Pour les échantillons, ils ont choisi 32 modèles de voitures et 10 caractéristiques de la conception automobile – nombre de cylindres, cylindrée, puissance brute, rapport de l’essieu arrière, poids, temps au ¼ mile, v/s moteur, transmission, nombre de vitesses et nombre de carburateurs.
Comme vous pouvez le constater, il existe une corrélation entre la variable de réponse mpg (miles per gallon) et certaines variables telles que le poids, la cylindrée, le nombre de cylindres et la puissance. Le problème peut être analysé en utilisant le paquetage glmnet dans R et la régression lasso pour la sélection des caractéristiques.
07. Analyse de régression du réseau élastique
Il s’agit d’un mélange de modèles de régression ridge et lasso formés avec les normes L1 et L2. Le filet élastique produit un effet de regroupement dans lequel les variables prédictives fortement corrélées ont tendance à entrer ou sortir ensemble du modèle. L’utilisation du modèle de régression du filet élastique est recommandée lorsque le nombre de prédicteurs est largement supérieur au nombre d’observations.
Veuillez noter que le modèle de régression du filet élastique a été créé en tant qu’option au modèle de régression lasso, car la section variable de lasso dépendait trop des données, ce qui la rendait instable. En utilisant la régression élastique nette, les statisticiens sont devenus capables de dépasser les pénalités de la régression ridge et lasso uniquement pour obtenir le meilleur des deux modèles.
Exemple
Une équipe de recherche clinique ayant accès à un ensemble de données de microréseaux sur la leucémie (LEU) souhaitait construire une règle de diagnostic basée sur le niveau d’expression des échantillons de gènes présentés pour prédire le type de leucémie. L’ensemble de données dont ils disposaient se composait d’un grand nombre de gènes et de quelques échantillons.
En outre, ils ont reçu un ensemble spécifique d’échantillons à utiliser comme échantillons d’entraînement, dont certains étaient infectés par une leucémie de type 1 (leucémie lymphoblastique aiguë) et d’autres par une leucémie de type 2 (leucémie myéloïde aiguë).
L’ajustement du modèle et la sélection des paramètres d’ajustement par CV décuplé ont été effectués sur les données d’apprentissage. Ils ont ensuite comparé les performances de ces méthodes en calculant leur erreur quadratique moyenne de prédiction sur les données de test afin d’obtenir les résultats nécessaires.
Utilisation de l’analyse de régression dans les études de marché
Une étude de marché se concentre sur trois matrices principales : la satisfaction du client, la fidélisation du client et la défense des intérêts du client. N’oubliez pas que si ces matrices nous renseignent sur la santé et les intentions des clients, elles ne nous indiquent pas les moyens d’améliorer la situation. Par conséquent, un questionnaire d’ enquête approfondi visant à demander aux consommateurs les raisons de leur insatisfaction est certainement un moyen d’obtenir des informations pratiques.
Cependant, il a été constaté que les gens ont souvent du mal à exprimer leur motivation ou leur démotivation ou à décrire leur satisfaction ou leur insatisfaction. En outre, les gens accordent toujours une importance excessive à certains facteurs rationnels, tels que le prix, l’emballage, etc. Globalement, il s’agit d’un outil d’analyse prédictive et de prévision dans le cadre des études de marché.
Utilisée comme outil de prévision, l’analyse de régression permet de déterminer les chiffres de vente d’une organisation en tenant compte des données externes du marché. Une multinationale réalise une étude de marché pour comprendre l’impact de divers facteurs tels que le PIB (produit intérieur brut), l’IPC (indice des prix à la consommation) et d’autres facteurs similaires sur son modèle de génération de revenus.
De toute évidence, l’analyse de régression en tenant compte des indicateurs de marketing prévus a été utilisée pour prédire les recettes provisoires qui seront générées au cours des prochains trimestres et même des prochaines années. Cependant, plus vous avancerez dans le futur, plus les données deviendront peu fiables, laissant une large marge d’erreur.
Étude de cas sur l’utilisation de l’analyse de régression
Une entreprise de purificateurs d’eau souhaitait comprendre les facteurs conduisant à la popularité de la marque. L’enquête était le meilleur moyen d’atteindre les clients existants et potentiels. Une enquête à grande échelle auprès des consommateurs a été planifiée et un questionnaire discret a été préparé à l’aide du meilleur outil d’enquête.
Un certain nombre de questions relatives à la marque, à la popularité, à la satisfaction et à l’insatisfaction probable ont été posées dans le cadre de l’enquête. Après avoir obtenu des réponses optimales à l’enquête, une analyse de régression a été utilisée pour réduire les dix principaux facteurs responsables de la favorisation de la marque.
Les dix attributs dérivés (mentionnés dans l’image ci-dessous) ont tous, d’une manière ou d’une autre, mis en évidence leur importance dans l’impact sur la popularité de cette marque spécifique de purificateur d’eau.

Comment l’analyse de régression permet-elle de tirer des enseignements des enquêtes ?
Il est facile d’effectuer une analyse de régression à l’aide d’Excel ou de SPSS, mais il faut alors comprendre l’importance des quatre chiffres dans l’interprétation des données.
Les deux premiers chiffres sur les quatre concernent directement le modèle de régression lui-même.
- Valeur F : Elle permet de mesurer la signification statistique du modèle d’enquête. Rappelons qu’une valeur F significativement inférieure à 0,05 est considérée comme plus significative. Une valeur F inférieure à 0,05 garantit que les résultats de l’analyse de l’enquête ne sont pas le fruit du hasard.
- R au carré : Il s’agit de la valeur selon laquelle les variables indépendantes tentent d’expliquer la quantité de mouvement des variables dépendantes. Si l’on considère que la valeur du R au carré est de 0,7, une variable indépendante testée peut expliquer 70 % de l’évolution de la variable dépendante. Cela signifie que les résultats de l’analyse de l’enquête que nous obtiendrons sont de nature hautement prédictive et peuvent être considérés comme précis.
Les deux autres nombres se rapportent à chacune des variables indépendantes lors de l’interprétation de l’analyse de régression.
- Valeur P : Comme la valeur F, la valeur P est également statistiquement significative. En outre, elle indique ici dans quelle mesure l’effet de la variable indépendante est pertinent et statistiquement significatif. Là encore, nous recherchons une valeur inférieure à 0,05.
- Interprétation : Le quatrième chiffre concerne le coefficient obtenu après avoir mesuré l’impact des variables. Par exemple, nous testons plusieurs variables indépendantes pour obtenir un coefficient. Elle nous indique « de quelle valeur la variable dépendante est censée augmenter lorsque les variables indépendantes (que nous considérons) augmentent d’une unité alors que toutes les autres variables indépendantes stagnent à la même valeur ».
Dans certains cas, le coefficient simple est remplacé par un coefficient normalisé qui démontre la contribution de chaque variable indépendante à l’évolution ou au changement de la variable dépendante.
Avantages de l’analyse de régression dans une enquête en ligne
01. Accéder à l’analyse prédictive
Savez-vous qu’utiliser l’analyse de régression pour comprendre les résultats d’une enquête auprès des entreprises revient à avoir le pouvoir de dévoiler les opportunités et les risques futurs ?
Par exemple, après avoir vu un créneau publicitaire particulier à la télévision, nous pouvons prédire le nombre exact d’entreprises en utilisant ces données pour estimer une offre maximale pour ce créneau. Le secteur de la finance et de l’assurance dans son ensemble dépend beaucoup de l’analyse de régression des données d’enquête pour identifier les tendances et les opportunités en vue d’une planification et d’une prise de décision plus précises.
02. Améliorer l’efficacité opérationnelle
Savez-vous que les entreprises utilisent l’analyse de régression pour optimiser leurs processus opérationnels ?
Par exemple, avant de lancer une nouvelle ligne de produits, les entreprises mènent des enquêtes auprès des consommateurs afin de mieux comprendre l’impact de différents facteurs sur la production, l’emballage, la distribution et la consommation du produit.
Une prévision fondée sur des données permet d’éliminer les conjectures, les hypothèses et les politiques internes de la prise de décision. Une meilleure compréhension des domaines ayant un impact sur l’efficacité opérationnelle et les revenus permet une meilleure optimisation de l’activité.
03. Aide quantitative à la prise de décision
Les enquêtes auprès des entreprises génèrent aujourd’hui un grand nombre de données relatives aux finances, aux revenus, aux opérations, aux achats, etc., et les chefs d’entreprise dépendent fortement de divers modèles d’analyse de données pour prendre des décisions commerciales éclairées.
Par exemple, l’analyse de régression aide les entreprises à prendre des décisions stratégiques éclairées en matière de main-d’œuvre. La réalisation et l’interprétation des résultats d’enquêtes auprès des salariés, telles que les enquêtes d’engagement des salariés, les enquêtes de satisfaction des salariés, les enquêtes d’amélioration de l’employeur, les enquêtes de départ des salariés, etc., permettent de mieux comprendre la relation entre les salariés et l’entreprise.
Il permet également de se faire une idée juste de certaines questions ayant un impact sur la culture et l’environnement de travail de l’organisation, ainsi que sur la productivité. En outre, des interprétations intelligentes orientées vers l’entreprise réduisent l’énorme quantité de données brutes en informations exploitables afin de prendre des décisions plus éclairées.
04. Prévenir les erreurs dues aux intuitions
En sachant comment utiliser l’analyse de régression pour interpréter les résultats d’une enquête, on peut facilement fournir un soutien factuel à la direction pour qu’elle prenne des décisions éclairées. Mais savez-vous qu’elle permet également d’éviter les erreurs de jugement ?
Par exemple, le directeur d’un centre commercial pense que s’il prolonge l’heure de fermeture du centre, les ventes augmenteront. L’analyse de régression contredit la croyance selon laquelle la prévision d’une augmentation des recettes due à une augmentation des ventes ne permettra pas de supporter l’augmentation des dépenses d’exploitation résultant de l’allongement de la durée du travail.
Conclusion
L’analyse de régression est une méthode statistique utile pour modéliser et comprendre les relations entre les variables. Il offre de nombreux avantages aux différents types de données et d’interactions. Les chercheurs et les analystes peuvent obtenir des informations utiles sur les facteurs influençant une variable dépendante et utiliser les résultats pour prendre des décisions éclairées.
Avec QuestionPro Research, vous pouvez améliorer l’efficacité et la précision de l’analyse de régression en rationalisant les processus de collecte, d’analyse et de rapport des données. L’interface conviviale de la plateforme et son large éventail de fonctionnalités en font un outil précieux pour les chercheurs et les analystes qui effectuent des analyses de régression dans le cadre de leurs projets de recherche.
Inscrivez-vous à l’essai gratuit dès aujourd’hui et laissez vos rêves de recherche s’envoler !









