 Reading Time: 5 minutes read
Reading Time: 5 minutes readPearson korelasyon katsayısı nedir?
Pearson korelasyon katsayısı veya Pearson korelasyon katsayısı veya Pearson’s r istatistikte iki değişken arasındaki ilişkinin gücünün ve birbirleriyle olan ilişkilerinin ölçümü olarak tanımlanır.
Basit bir ifadeyle, Pearson korelasyon katsayısı, bir değişken değiştiğinde diğer değişkendeki değişimin etkisini hesaplar.
Örneğin: Belirli bir yaşa kadar, (çoğu durumda) bir çocuğun boyu yaşı arttıkça uzamaya devam edecektir. Elbette, büyümesi genler, konum, beslenme, yaşam tarzı vb. gibi çeşitli faktörlere bağlıdır.
Bu yaklaşım kovaryansa dayanmaktadır ve bu nedenle iki değişken arasındaki ilişkiyi ölçmek için en iyi yöntemdir.
Pearson korelasyon katsayısı testi ne işe yarar?
Pearson katsayısı korelasyonu yüksek bir istatistiksel anlamlılığa sahiptir. İki değişken arasındaki ilişkiye bakar. Aralarındaki ilişkiyi göstermek için iki değişkene ait veriler üzerinden bir çizgi çizmeye çalışır. Değişkenler arasındaki ilişki Pearson korelasyon katsayısı hesaplayıcısı yardımıyla ölçülür. Bu doğrusal ilişki pozitif veya negatif olabilir.
Örneğin:
- Pozitif doğrusal ilişki: Çoğu durumda, evrensel olarak, bir kişinin yaşı arttıkça geliri de artar.
- Negatif doğrusal ilişki: Araç hızını artırırsa, seyahat için geçen süre azalır ve bunun tersi de geçerlidir.
Yukarıdaki örnekten, Pearson korelasyon katsayısı r’nin iki şeyi bulmaya çalıştığı açıktır – verilen örnek boyutlarından ilişkinin gücü ve yönü.
Pearson korelasyon katsayısı formülü
Korelasyon katsayısı formülü, değişkenler arasındaki ilişkiyi ortaya çıkarır. -1 ile 1 arasındaki değerleri döndürür. İki değişkenin gücünü ölçmek için aşağıdaki Pearson katsayısı korelasyon hesaplayıcısını kullanın.
Pearson korelasyon katsayısı formülü:
Nerede?
N = puan çiftlerinin sayısı
Σxy = eşleştirilmiş puanların çarpımlarının toplamı
Σx = x puanlarının toplamı
Σy = y puanlarının toplamı
Σx2 = karesi alınmış x puanlarının toplamı
Σy2 = y puanlarının karelerinin toplamı
Pearson korelasyon katsayısı hesaplayıcısı
İşte Pearson korelasyon katsayısını hesaplamak için adım adım bir kılavuz:
Birinci adım: Bir Pearson korelasyon katsayısı tablosu oluşturun. Her iki değişkeni de içeren bir veri grafiği oluşturun. Bu değişkenleri ‘x’ ve ‘y’ olarak etiketleyin. Üç ek sütun ekleyin – (xy), (x^2) ve (y^2). Bu basit veri tablosuna bakın.
İkinci adım: Tabloyu tamamlamak için temel çarpma işlemini kullanın.
Üçüncü adım: Aşağıdan yukarıya doğru tüm sütunları toplayın.
Dördüncü adım: Değerleri girmek için korelasyon formülünü kullanın.
Sonuç negatifse, iki değişken arasında negatif bir korelasyon ilişkisi vardır. Sonuç pozitif ise, değişkenler arasında pozitif bir korelasyon ilişkisi vardır. Sonuçlar ayrıca doğrusal bir ilişkinin gücünü de tanımlayabilir, yani güçlü pozitif ilişki, güçlü negatif ilişki, orta pozitif ilişki vb.
Pearson Momentler Çarpımı Korelasyon Katsayısının Gücünün Belirlenmesi
Pearson momentler çarpımı korelasyon katsayısı ya da kısaca Pearson korelasyon katsayısı veya Pearson korelasyon katsayısı r, iki değişken arasındaki doğrusal ilişkinin gücünü belirler. İki değişken arasındaki ilişki ne kadar güçlüyse, cevabınız 1 veya -1’e o kadar yakın olacaktır. 1 veya -1 değerlerinin elde edilmesi, tüm veri noktalarının ‘en iyi uyum’ doğrusu üzerinde çizildiğini gösterir. Bu, herhangi bir değişkenin faktörlerindeki değişimin diğer değişkenle olan korelasyonu zayıflatmadığı anlamına gelir. Cevabınız 0’a ne kadar yakınsa, değişkenlerdeki varyasyon o kadar fazladır.
Pearson korelasyon katsayısı nasıl yorumlanır?
Aşağıda Pearson katsayısı korelasyonunun yorumlanması için önerilen yönergeler yer almaktadır:
Değişkenler arasındaki ilişkinin gücünün neyi ölçtüğünüze ve örneklem büyüklüğüne bağlı olduğunu unutmayın.
Bir grafik üzerinde, değişkenler arasındaki ilişki fark edilebilir ve daha hesaplama yapmadan varsayımlarda bulunulabilir. Dağılım grafikleri, eğer doğruya yakınsa, değişkenler arasında güçlü bir ilişki olduğunu gösterir. Dağılım grafikleri doğruya ne kadar yakınsa, değişkenler arasındaki ilişki o kadar güçlüdür. Çizgiden ne kadar uzaklaşırlarsa, ilişki o kadar zayıflar. Eğer çizgi x eksenine neredeyse paralelse, grafik üzerine rastgele yerleştirilmiş dağılım grafikleri nedeniyle, iki değişken arasında korelasyon olmadığını varsaymak güvenlidir.
Güç ve yön terimleri ne anlama geliyor?
‘Güç’ ve ‘yön’ terimleri istatistiksel bir öneme sahiptir. İşte iki kelimenin basit bir açıklaması:
- Güçlü: Güç, iki değişken arasındaki ilişki korelasyonunu ifade eder. Bir değişkenin diğerindeki değişime bağlı olarak ne kadar tutarlı bir şekilde değişeceği anlamına gelir. +1 veya -1’e yakın değerler güçlü bir ilişkiye işaret eder. Bu değerlere, veri noktaları doğrunun üzerine veya çok yakınına düştüğünde ulaşılır. Veri noktaları ne kadar uzaklaşırsa, doğrusal ilişkinin gücü de o kadar zayıflar. Veri noktaları dağınık olduğu için düz bir çizgi çizmenin pratik bir yolu olmadığında, doğrusal ilişkinin gücü en zayıftır.
- Yön: Doğrunun yönü, değişkenler arasında pozitif doğrusal veya negatif doğrusal bir ilişki olduğunu gösterir. Eğer çizgi yukarı doğru bir eğime sahipse, değişkenler arasında pozitif bir ilişki vardır. Bu, bir değişkenin değerindeki artışın diğer değişkenin değerinde de artışa yol açacağı anlamına gelir. Negatif bir korelasyon aşağı doğru bir eğimi gösterir. Bu, bir değişkenin miktarındaki artışın başka bir değişkenin değerinde azalmaya yol açtığı anlamına gelir.
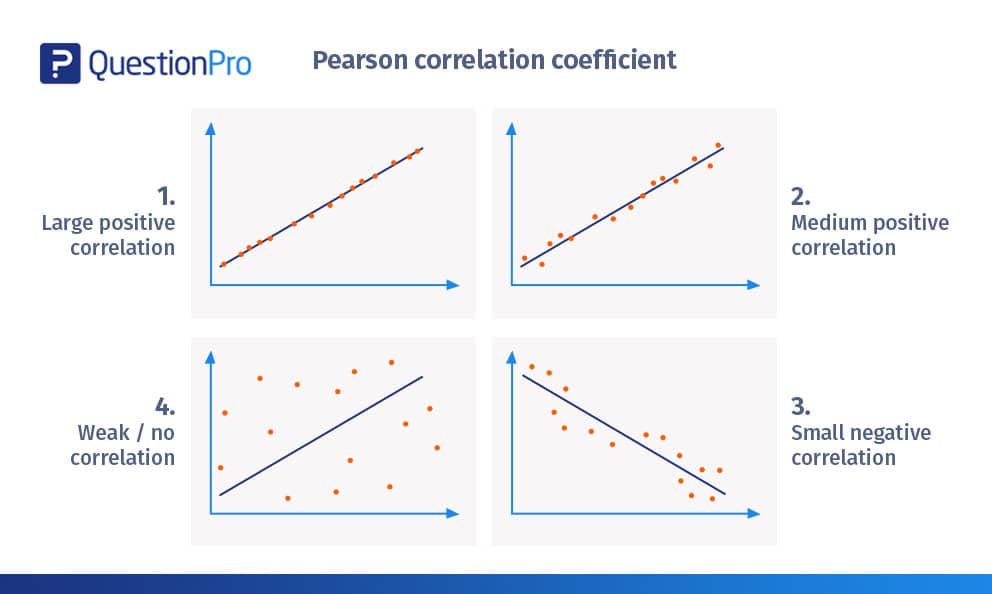
Pearson korelasyon katsayısı örnekleri
Pearson korelasyon katsayısı tablosunu yorumlamanıza yardımcı olacak bazı görsel örneklere bakalım:
- Büyük pozitif korelasyon:
Yukarıdaki şekil neredeyse +1’lik bir korelasyon göstermektedir.
Dağılım grafikleri neredeyse düz çizgi üzerinde çizilmiştir.
Eğim pozitiftir, yani bir değişken artarsa diğer değişken de artar ve pozitif doğrusal bir çizgi gösterir.
Bu, bir değişkendeki değişimin diğer değişkendeki değişimle doğru orantılı olduğunu gösterir.
Büyük bir pozitif korelasyona örnek olarak şunlar verilebilir: – Çocuklar büyüdükçe giysi ve ayakkabı numaraları da büyür.
Pearson korelasyon katsayısı tablosunu yorumlamanıza yardımcı olacak bazı görsel örneklere bakalım:
- Orta düzeyde pozitif korelasyon:
Yukarıdaki şekil pozitif bir korelasyonu göstermektedir.
Korelasyon +0,8’in üzerinde ancak 1+’nın altındadır.
Oldukça güçlü bir doğrusal yokuş yukarı desen gösterir.
Orta düzeyde pozitif korelasyona örnek olarak şu verilebilir: – Otomobil sayısı arttıkça yakıt değişkenine olan talep de artar.
- Küçük negatif korelasyon
Yukarıdaki şekilde, dağılım grafikleri önceki örneklere kıyasla düz çizgiye o kadar yakın değildir
Yaklaşık -0,5’lik negatif doğrusal bir korelasyon gösterir.
Eğim negatif olduğu için bir değişkendeki değişim diğer değişkendeki değişimle ters orantılıdır.
Küçük bir negatif korelasyon örneği şöyle olabilir: – Birisi ne kadar çok yerse, o kadar az acıkır.
- Zayıf / korelasyon yok
Dağılım grafikleri çizgiden çok uzakta.
Pratikte bir sınır çizmek zordur.
Korelasyon yaklaşık +0,15’tir
Bir değişkendeki değişimin diğer değişkenle doğru orantılı veya ters orantılı olduğuna karar verilemez.
Zayıf/ilişkisiz ilişkiye örnek olarak – Yakıt fiyatlarındaki artış daha az insanın evcil hayvan edinmesine yol açar.



















