ピアソン相関係数。自由な例| QuestionPro

ピアソン相関係数とは何ですか？

ピアソン相関係数またはピアソンのrは、統計学において、2つの変数間の関係の強さと互いの関連性を測定するものとして定義されています。

簡単に言うと、ピアソンの相関係数は、ある変数が変化したときに、もう一方の変数が変化したときの影響を計算するものです。

例えば、こんな感じです。 ある年齢までは、（多くの場合）年齢が上がるにつれて身長はどんどん伸びていきます。もちろん、遺伝子、場所、食事、生活習慣など、さまざまな要因によって成長は異なります。

この方法は共分散に基づくため、2つの変数の関係を測定するのに最適な方法である。

ピアソン相関係数検定は何をするものですか？

ピアソン係数の相関は、統計的に高い有意性を示した。 2つの変数の関係を見るものである。 2つの変数のデータを線で結び、その関係を示そうとするものである。変数の関係は、ヘルプピアソン相関係数の計算機で測定されます。この線形関係は正にも負にもなりうる。

例えば、こんな感じです。

正の直線関係。ほとんどの場合、普遍的に、年齢が上がるにつれて収入が増える。
負の直線関係。 車速を上げると走行時間が短くなり、逆に車速を下げると走行時間が長くなる。

上の例から、ピアソンの相関係数であるrは、与えられたサンプル数から関係の強さと方向性の2つを見つけようとするものであることがわかる。

ピアソン相関係数の計算式

相関係数の式は、変数間の関係を見つけるものです。 1から1までの値を返します。 2つの変数の強さを測定するために、以下のピアソン係数相関計算機を使用してください。

ピアソン相関係数の計算式。

どこで

N = スコアのペアの数

Σxy = 対のスコアの積の総和

Σx = xの得点の合計

Σy = yの得点の合計

Σx2 = xのスコアの2乗の和

Σy2 = yの得点の二乗の和

ピアソン相関係数計算機

ここでは、ピアソンの相関係数の計算方法をステップバイステップで説明します。

ステップ1 ピアソン相関係数表を作成する。両方の変数を含むデータグラフを作成する。これらの変数に ‘x’ と ‘y’ のラベルを付ける。(xy)、(x^2)、(y^2)の3つの列を追加する。この簡単なデータ表を参考にしてください。

ステップ2 基本的な掛け算を使って表を完成させる。

ステップ3。下から上へすべての列を足し算します。

ステップ4相関式を使って、値を差し込む。

結果が負の場合、2つの変数の間には負の相関関係がある。結果が正であれば、変数間に正の相関関係があることになる。結果は、線形関係の強さ、すなわち、強い正の関係、強い負の関係、中程度の正の関係、などを定義することもできる。

ピアソン積率相関係数の強さを決定する

ピアソン積率相関係数、または単にピアソン相関係数あるいはピアソン係数相関rは、2つの変数の間の線形関係の強さを決定する。 2つの変数の関連性が強ければ強いほど、答えは1または-1に傾くでしょう。 1または-1の値を得ることは、すべてのデータポイントが「最適な適合」の直線上にプロットされることを意味する。これは、いずれかの変数の係数が変化しても、他の変数との相関が弱まらないことを意味する。答えが0に近いほど、変数のばらつきが大きいことを意味します。

ピアソン相関係数の解釈の仕方

以下は、ピアソン係数相関の解釈のガイドライン案です。

変数の関連の強さは、測定するものやサンプルサイズに依存することに注意してください。
グラフでは、変数間の関係に気づき、計算する前に仮定を立てることができる。散布図が直線に近い場合、変数の間に強い関係があることを示している。散布図が直線に近いほど、変数の関係が強いことを意味する。線から離れるほど、関係は弱くなる。グラフ上にランダムに配置された散布図により、線がx軸にほぼ平行であれば、2つの変数に相関はないと考えてよいでしょう。

強度と方向性という言葉の意味は何ですか？

強さ」と「方向性」は統計的な意味を持つ言葉です。ここでは、この2つの言葉についてわかりやすく解説します。

強さです。 強さは、2つの変数の関係相関を意味する。一方の変数の変化により、もう一方の変数がどれだけ一貫して変化するかを意味します。値が+1または-1に近いほど、強い関係であることを示す。この値は、データ点が直線上、または直線に非常に近いところにある場合に達成される。データポイントが離れるほど、直線関係の強さは弱くなる。データポイントが散在しているため、現実的に直線を引く方法がない場合、直線関係の強さは最も弱くなる。
方向性直線の方向は、変数間の正の線形関係または負の線形関係を示す。直線が上向きの傾きを持つ場合、変数は正の関係を持っています。つまり、ある変数の値が増加すれば、もう一方の変数の値も増加することになる。負の相関は、下降線を意味する。つまり、ある変数の量の増加は、別の変数の値の減少につながる。

無料アカウント作成

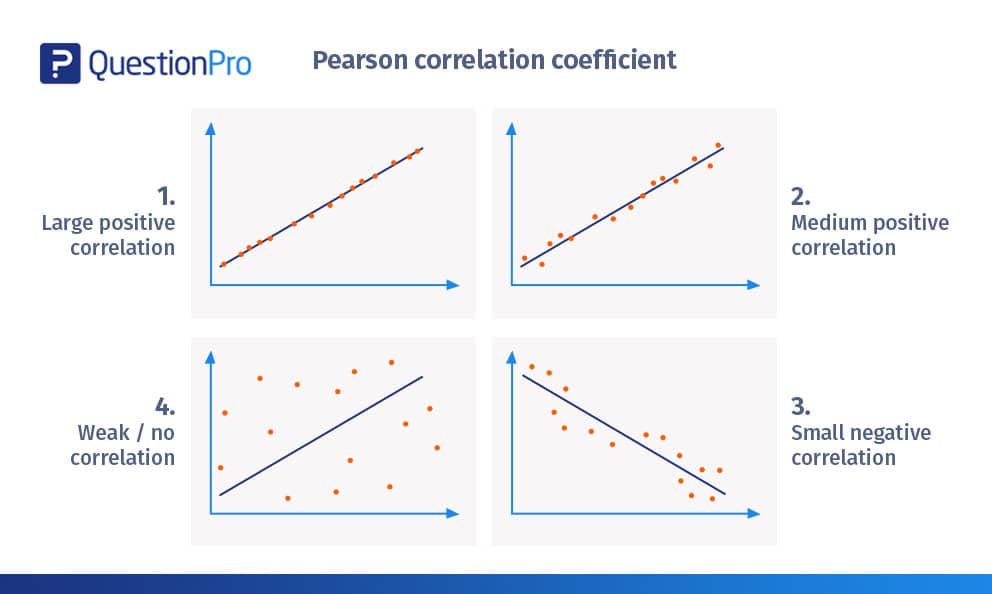
ピアソンの相関係数の例

ピアソン相関係数表を解釈するための視覚的な例をいくつか見てみましょう。

大きな正の相関がある。

上の図は、ほぼ+1の相関を描いています。
散布図はほぼ直線上にプロットされている。
傾きが正であることから、一方の変数が増加すれば、もう一方の変数も増加し、正の直線を示している。
これは、一方の変数の変化が他方の変数の変化に正比例することを示す。
大きな正の相関がある例として、「子供が成長すると、服や靴のサイズも大きくなる」というものがあります。
ピアソン相関係数表を解釈するための視覚的な例をいくつか見てみましょう。